Theory of relativity has a problem!
The real world is much simpler (and much less bizarre), then “relativistic” scientists say.
Mathematics of a “simple” trigonometry reliably describes whole (space) mechanics, “mysterious” spacetime, time-dilatation and the phenomenon of gravity as well … nothing more is needed (whatever more is wrong).
THE MASS OF THE MOON (1.3 SECONDS AWAY) IS 2.3 PICOSECONDS!
„Make everything as simple as possible, but not simpler.“
Albert Einstein
Does the headline sound odd to you? No reason for that:
In fact, the terms second, meter or kilogram are only unit terms, implemented by humankind gradually (over the time of our civilization’s development) – in connection to economic creation (the development of commerce). So can’t we just agree to make the terminology easier and measure time, length and matter only in seconds?
Inter alia, this new convention will help us to simplify physics, eliminate useless physical constants and understand the mechanics, gravity and spacetime phenomena more correctly:
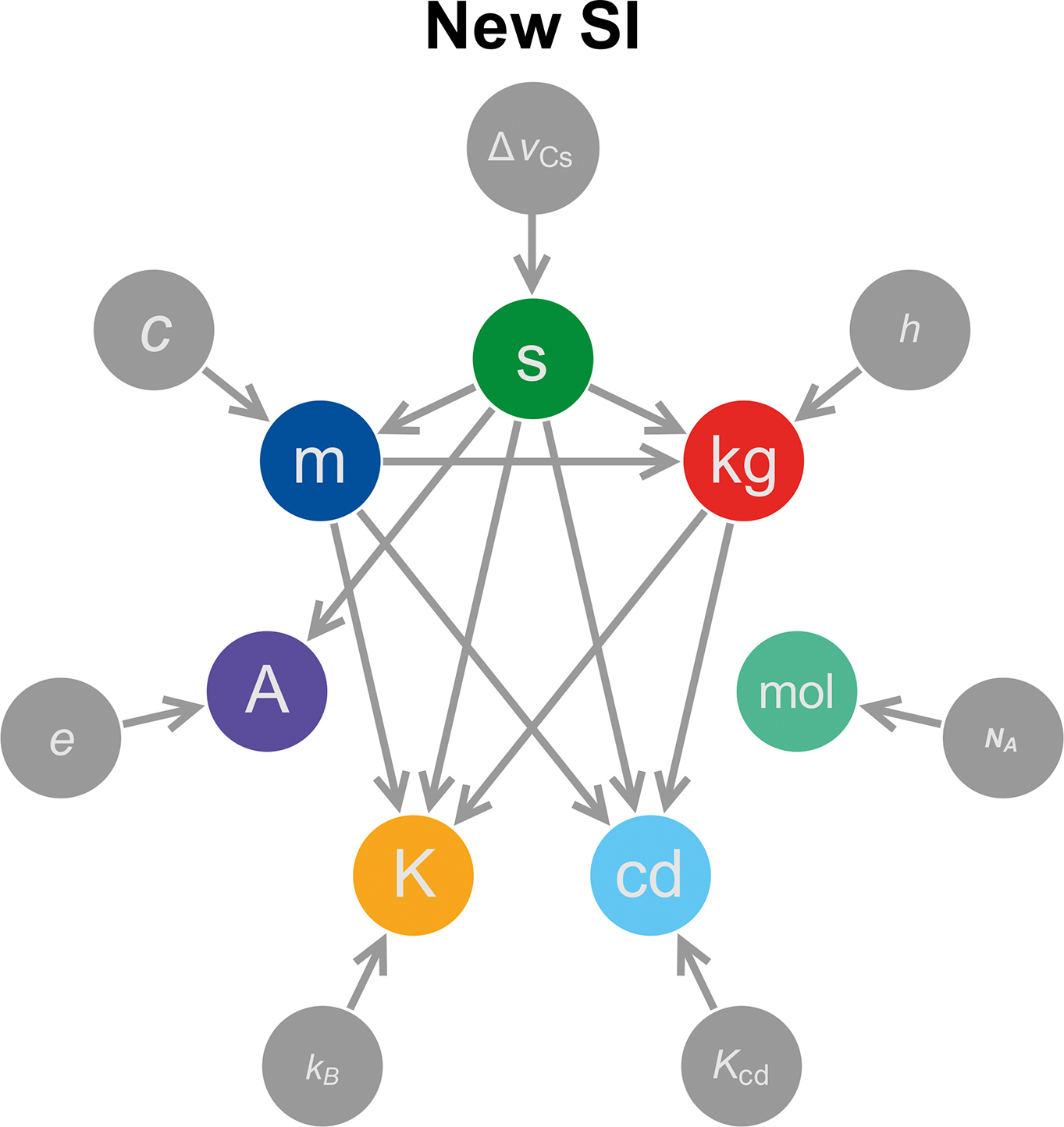
1 “SI” UNITS AND A NEW DEFINITION OF KILOGRAM
A couple of years ago, the International Bureau of Weights and Measures (CIPM) proposed a crucial change in the definition of base physical units, whose implementation is planned for the year 2018. This should be a fundamental revolution of the International System of Units (SI), as no physical unit is going to be defined according to the obsolete “etalon” – all seven units will be derived from unchangeable laws of nature. The majority of units (except for the second and meter) will thus be redefined by the “connected” physical law.
The new definition of the seven base units requires the setting of seven key physical constants, whose “fixing” will lead subsequently to the exact definition of related physical units:
Picture 154:
From 2018, almost everything will be different.
(Source: Wikimedia)
The biggest change will be related to the kilogram – the only and last unit that still depends on comparison with the etalon (stored in a Parisian safe box), which loses a microgram of its mass during every cleaning procedure. So the kilogram also needs “its” new physical constant (through which it will be defined) – this constant is the Planck constant (h):
Kaufmann’s, Einstein’s and Planck’s synergic efforts led us to the knowledge of the energy equation (m c2 = h f) a century ago, revealing the physical connection between mass and the Planck constant.
We have already been able to measure time (frequency) and the second very accurately for decades, … on the basis of the second, we also subsequently defined the meter (by fixing the speed of light), … so now we are able to accurately set (fix) the value of the Planck constant to define the new kilogram.
A couple of successful experiments were conducted for this purpose (over the past months and years) to precise the Planck constant, whose primary principle were the so-called watt (Kibble) balance:
During such an experiment, an energetic (power) or force balance is achieved on the measuring device in the gravitational field of the Earth, while these newly created devices work “bidirectionally” – in the first, their purpose was to make the Planck constant (under known mass) more accurate, while in the future, they will be used for mass measurement (under the well-known and fixed Planck constant), or for production of new mass etalons (for the industry and services areas).
Base physical units (and their value) will soon create a “revolutionary” and more precise system.
… or is it only an evolution?
2 PHYSICS REMAINING BEHIND…
Although physics likes to consider itself as the privileged “princess of science” (the queen of science is mathematics), its privileged status on the imaginary scientific throne is somehow illusionary. Even the quote: “mathematics is the language of physics” is not every meaningful – mathematics is the language of all scientific fields today.
Mathematics is the “queen of science” because it was developed as the first science in prehistoric nations (it was necessary to count the hunted animals and enemy warriors), and therefore it is more than tens of thousands years older than the other sciences. Only when (around 10 thousand years ago) the last ice age ended, people in Mesopotamia started to develop agriculture, Sumerians later (ca 4000 BC) created the first civilized society (the division of labour, social hierarchy, overproduction of resources, commerce, …) – and so the second scientific field was developed – economics (where mathematics served bartering and land measurements). As time went on, other nations (mainly the Babylonians and Egyptians) improved upon mathematics (arithmetic, geometry and algebra), while the “business” always was the motive of progress (not the need for “science”) – accounting was developed (in grain, beer or silver units) as well as loans, interest and taxes – but even in this case, it always was primarily about accumulation of property (and about power)!
On the same basis (GDP growth), almost in parallel with economics, astronomy was developed (a calendar is necessary for planning in agriculture, military action and tax payments), which we consider today as being a “natural” part of physics. In fact, we can speak about the birth of physics only in Ancient Greece (ca 600 BC), where (together with philosophy birth) the first complex theories about the nature of our world, laws of motion (mechanics) and first models of the univers were born. “Physics” in the current sense is only ca 400 years “old”.
The factual young age (immaturity) of physics may also be demonstrated in the fact, that mathematics and economics may be studied today even from textbooks that are 100 years old, whereas in physics, everything is constantly changing!
A transparent and long-lasting conflict in physics these days is the large number of base units and related constants, pointing to a certain “non-systemic” approach:
Economics has also had a number of constants throughout history (how many peaches per dozen plums, how many beers per bag of barley, how much bread per day of work), but as time passed, the situation was resolved by the “invention” of money, so the number of base units and constants dropped significantly (how many plums, peaches, beers, barleys, bread or days of work per Mexican dollar or Pound sterling) and globalization caused a further decrease of such base units (currencies) and their constants (currency rates). These days – economics is aiming for one and only (universal) base unit (whether it will be USD, EUR, CNY or BTC) – in which it is possible to measure everything – economic power, goods, human work, health injury or your goodwill. Such an economy does not need any constant!
At the start of the third millennium, we find science a little inconsistent, as some scientific fields have not finished their “globalization” or systemization yet:
Precisely abstract mathematics has (of course) 0 units and 0 constants (π or e are not constants, but irrational numbers, whose value can be mathematically derived).
Economics points to just 1 unit and 0 constants.
What about physics?
After the implementation of the entire progress (2018), we will have 7 base units and 7 constants, while we also have tens of derived units and other constants! Even just mechanics itself claims 3 base units and 3 constants.
Isn’t it too much?
3 THE MOON IS AT A DISTANCE OF 1.3 SECONDS!
It is relatively easy to make the first step:
In fact, meter or second are only terms – created by society’s need to standardize the expression for space and time “distance” – for length and time “space”. Many nations on our planet instead use yards, miles, inches or couls for length measurement. In the same way, for time measurement (besides seconds) we may find for example the helek (Hebrew unit of time).
So can’t we just make an agreement – to measure time and space in seconds?
Many readers may see such an idea as heretic and senseless. Can the meter lying in Paris in the form of metallic etalon (in the safe deposit of the International Bureau of Weights and Measures) be replaced by a second and can we subsequently measure distance with stopwatches or an atomic clock? Maybe older readers can remember their school knowledge – the definition that a meter expresses one ten-millionth of an earth quadrant (half a meridian). What can that have in common with a second?

Picture 155:
Meter etalon
(Source: Wikimedia)
Space and time are such close categories that even our ancients often measured distance in time. Old sea-farers used to express the distance between continents by the number of days of the voyage. Many readers have already heard the response to the question “How far is it?” as “Approximately 10 minutes”. Would you argue that this is only a folk (non-scientific) expression?
In the highly prestigious scientific field of astronomy, the verified unit for distance is the light year!
Time (the second) is very closely related to the length (the meter). Their relation is in fact so close that the newest international definition (SI) – defines the meter just by using time:
1 meter is the length of the path travelled by light (in a vacuum) in 1/299 792 458 seconds.
This “odd” constant of 299 792 458 does not represent anything “general” or mystical (that should be worshipped) – it is only a proof, how non-systemically people constructed etalons for time and length – it reflects the reality, that there is no causal relation between the rotation of our planet and the length of its meridian.
Therefore, there is nothing that would hinder us from selecting a more meaningful unit of length and reformulating the abovementioned definition for better comprehension:
299 792 458 meters is the length of the path travelled by light (in a vacuum) per time length of 1 second.
So reciprocally, in a reduced and mathematical form, it can be defined in the following way:
1 second = 299 792 458 meters
If we define the unit of length by time, why not measure it in seconds?
So why not describe time and length distance in the same way? What is hindering us from unifying these two units? Why make physics and related mathematics harder and why have to remember the completely useless constant (c = 299 792 458 m/s)?
You may argue that such a length second would be too large? That’s relative:
The length of 299 792 458 may seem to be large just from the “human” point of view (the Moon is only a little more distant from the Earth), but in a cosmic scale, this is a very insignificant distance, with the second also being insignificant in comparison with the entire history of the universe. Even within the astronomical observations of our galaxy, the light year (ca 9.5×1015 metres) serves the best purpose for astronomers!
Even – astronomers do not use the entire combination “light year” in common expressions. They tend to proclaim the following automatically: “This star is 12 years distant”. It is completely clear to everyone (from the context) that it’s an expression for the length distance and everyone can verify with a calculator that it’s ca 1.1×1017 meters.
Why waste words?
In light of the abovementioned, in harmony with the SI definition (and with reference to a common human intellect), it will be more appropriate to use the second for the space distance expression!
The use of this terminology will make many things easier. And it’s not only about wasting words. The following chapters will reveal more …
At this point, it will be enough to accept the fact that the Moon is at a distance of 1.3 seconds!
4 THE MOON HAS A MASS OF 2.3 PIKOSECONDS!
The second step requires even more “courage” and abilities to go against the “traditions”. Even this step is strictly logical:
All the methods of mass measurement by now prefer just one “side” of matter – gravity mass!
If we speak about kitchen, laboratory or watt scales (see the chapter “SI” units and new definition of kilogram) – their principle is always the force effects within a gravitational field, which is never “universal”, but only local. The consequence of this fact is also the main problem of current (traditional) mass measurement:
On Earth, on the Moon or on Mars, our measurement devices will provide us with different values, while on the ISS space station (or falling plane), they won’t work!
So wouldn’t it be more meaningful to use something “universal” for the definition of mass (working within the entire universe), and therefore also more reliable?
Because matter has one more way of its expression – inertia!
Mass means the value, by which we may measure inertial or gravitational effects of matter. To push a heavier car requires greater effort (inertial mass), while lifting a heavier object (within a gravitational field) also requires more effort (gravitational mass). Newton already knew that both mass effects are equivalent.
Inertial mass is universal – it works everywhere!
An astronaut (on the ISS space station) may easily “lift” for example even a 500 kg iron ball (unlike on Earth), however he will crush his toe when trying to kick it to his fellow (as painful as on Earth) – even without gravity – the ball wants to stay in its original place.
Thus, we are getting closer to the key question:
How can we compare the mass of two items universally (so even on the ISS)?
Many thousands of years ago, humankind solved a similar question successfully (on Earth) by using the balancing scales, but these are able to measure only gravitational mass, so they are useless on the ISS space station.
So which physical measurements can astronauts use to be able to compare mass of bodies? What can we use to measure mass under conditions without gravity? There is only one correct response to such questions:
We have to measure TIME!
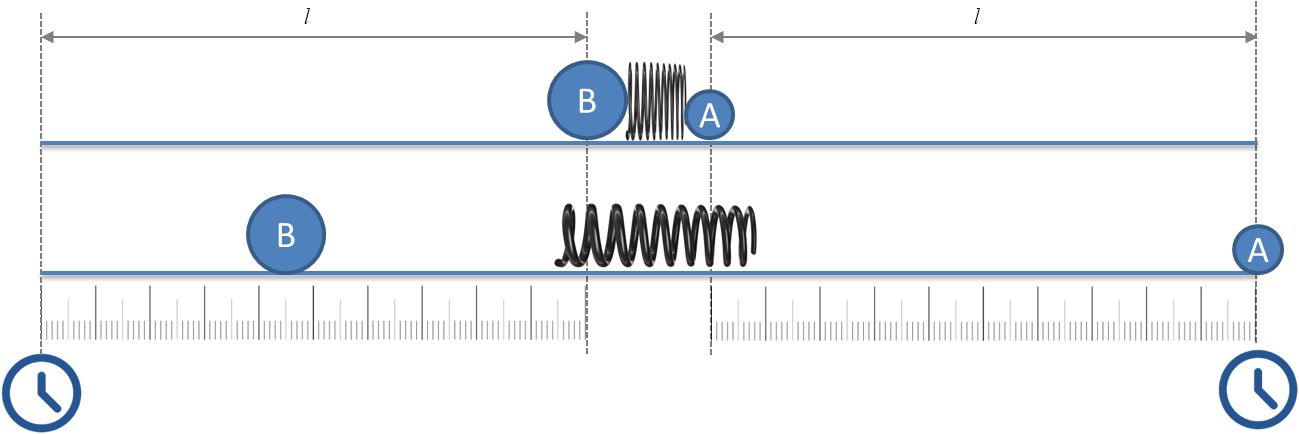
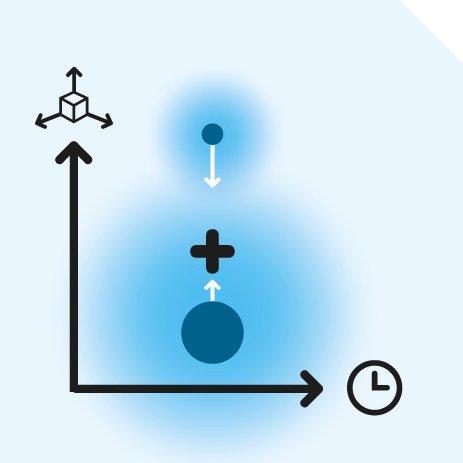
… for example on the balancing inertial scales:
Picture 156:
Principle of balancing inertial scales
It is not important which source of energy we use to move both bodies (the spring may be replaced for example by the explosive principle) – the key for the entire device is the mass symmetry of motion (the law of conservation of momentum) – the body of lower mass will reach the destination (arm length) in a shorter time, while the ratio of both times will be directly proportional to the ratio of masses:
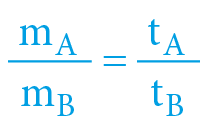
So if we have a body of known mass (etalon) on one side, it will be easy to determine the mass of the other body – it will always be directly proportional to the measured time!
And it will be the same as in the case of balancing scales – later we will surely construct “single-arm” measuring devices determining the body (of unknown mass) momentum, known to us. Analogically to watt scales – an electromagnetic “cannon” will be constructed, which (on the basis of Planck law) will assign known momentum to the body … and by measuring the time necessary to overcoming a certain distance – it will calculate the mass reliably.
And it will be function able everywhere – on Earth, on the Moon, on Mars or in whichever part of the deepest universe. So the primary principle of every “universal” mass measurement will be time measurement – the universal unit of mass will be the second!
After all – the fact that mass may be measured by time can be already seen in our everyday life as well (outside of the physical laboratory):
If you shovel sand from one pile to another – you may say: “I have 2 hours’ worth of sand here”. Even in the event that you go for a hike in the mountains – increasing the weight of your bag will cause a greater journey time. Naturally – these examples are provided with a certain degree of exaggeration (other physical factors have an effect too) – but they still reflect the physical relations and “tell us” that matter may be measured by time!
Moreover – real experiments in particles accelerators are a further “hint” – the mass of the objects rises in relation to the speed by exactly the same ratio as time dilation!
So we now have to determine mass of the “mass second” etalon – so that traditional physics may be simplified again and other “constant” let disappear (G = 6.67408 × 10−11 m3 kg−1 s−2).
Here, we will leave long explanations and deductions (the next chapter will reveal why it can’t be otherwise):
1 second = c3/(4 π G) ≅ 3.2×1034 kilogram
Someone could again argue that selecting such a “huge” value for the unit of mass may be “crazy” – because even the most massive known star in the universe (R136a1) has a mass of only 0.02 seconds. Even in this case – it’s necessary to overcome the “traditions and customs” to open our eyes and discover that within the context of our known universe, the time second (see the second needle), length second (3×108 metres) and mass second (3×1034 kg) are suspiciously proportional – see later.
Let’s admit that mass could be better measured in seconds:
And we have to emphasize now that it’s more than “only” a simplification of some physical formulas and elimination of some useless constants. It’s more than just accepting the fact that the Moon has a mass of 2.3 picoseconds …
… this all has to be done primarily to finally better understand to SPACETIME!
5 SPACETIME AND TRIGONOMETRY
The term “spacetime” is over 100 years old and is still (for the population, but also for many physicists) somewhat unclear – it’s hard to imagine it, hard to grasp it and it’s somehow schizophrenic:
When Minkowski “invent” it for the first time (1907), he did so within traditional (used for centuries) Euclidean space, where Pythagorean Theorem is valid and the sum of angles (within a triangle) is equal to π (180°). In fact, spacetime became popular thanks to Einstein only (in 1916), when he used it as the base for his General theory of relativity, where spacetime in a non-Euclidean – is curved. As a result, spacetime is a somewhat “bipolar” category these days:
4000 years ago, we were able to map fields, lands, continents, the Earth, our Solar System, our galaxy and almost the entire universe successfully by using Euclidean (non-curved) geometry … however, Einstein’s relativity postulates that spacetime is curved for the purpose of gravitation explanation, while the universe itself is (according to the actual cosmology) Euclidean (non-curved).
So – where’s the truth? Is it really necessary to curve spacetime to explain gravity?
By the rationalization (merging) of all three units of mechanics into one (second), we may encounter a very exciting connection between trigonometry and 4D spacetime. If we measure in seconds – everything will be simplified and “revealed” to such an extent – that the entire spacetime mechanics (incl. gravity!) may be described by “simple” trigonometry:
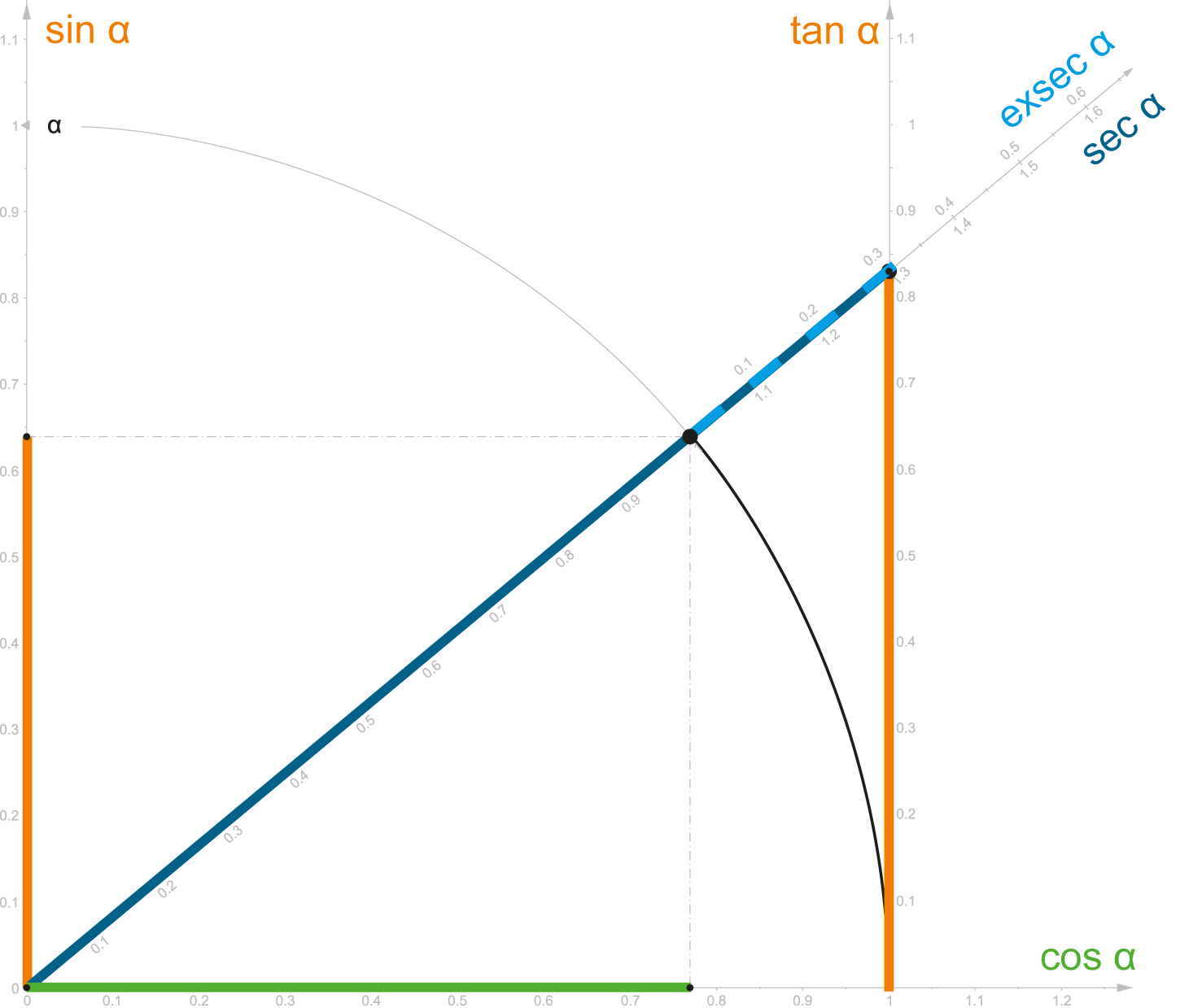
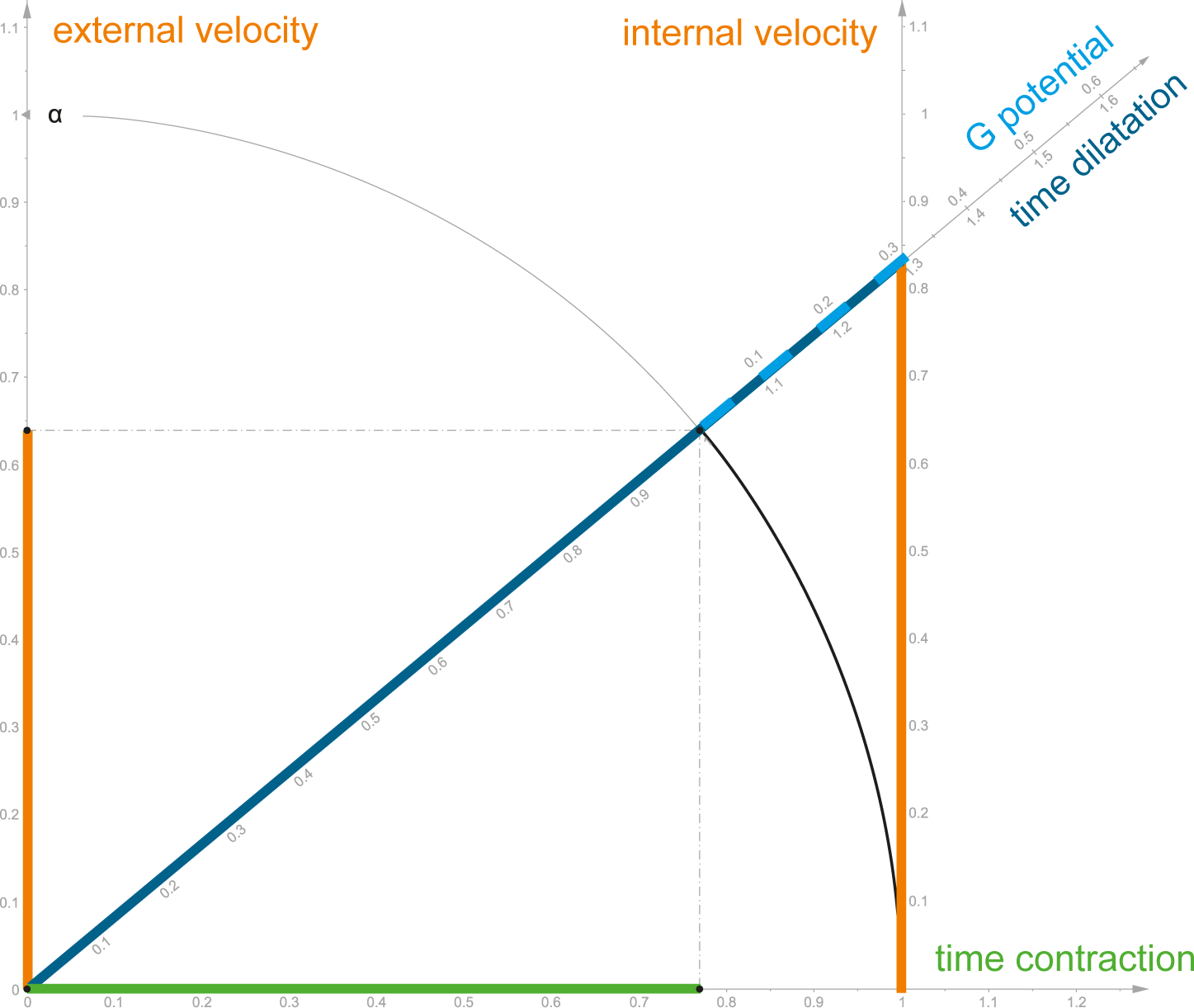
Picture 157:
Geometry of Euclidean space
Picture 158:
Geometry of spacetime mechanics
Yes!
Euclidean geometry and spacetime geometry are identical (in this new concept) – both are describing by the basic trigonometric functions. The key physical quantities of mechanics (in a 4D spacetime) are directly described by single trigonometric functions.
And as Pythagorean Theorem is the basis of trigonometry, all the single values may be calculated between each other by using the trigonometric functions or by Pythagorean Theorem:
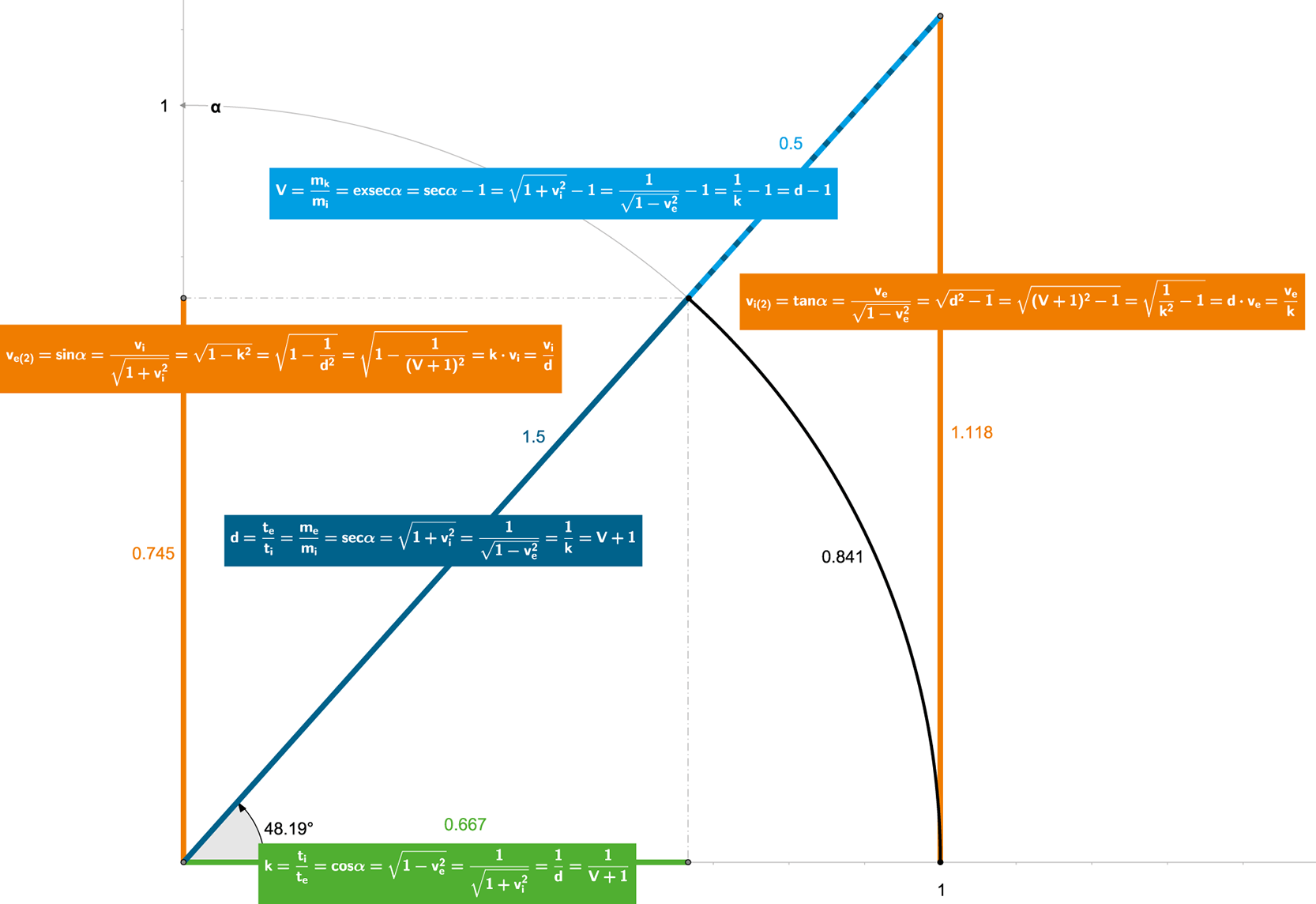
Picture 159:
INTERACTIVE ANIMATION
First graphical visualization of gravitational phenomenon in the history of mechanics and quantification of the scenario: “How the Sun never changed into a black hole!” at the same time.
αspacetime angle – the ratio of spacetime motion (induced by gravity) [1]
Vgravitational potential [1]
ve(2)external escape (2. cosmic) velocity [1]
vi(2)internal escape (2. cosmic) velocity [1]
k time contraction [1]
d time dilation [1]
tiinternal time [s]
teexternal time [s]
miinternal (primary rest) mass [s]
meexternal (total apparent) mass [s]
mkkinetic mass [s]
All the mathematical relations can be found in the figure above, but the most important we have to mention again:
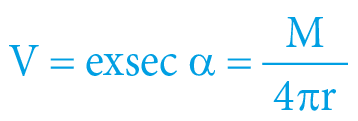
d = sec α = V + 1
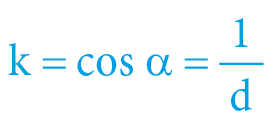
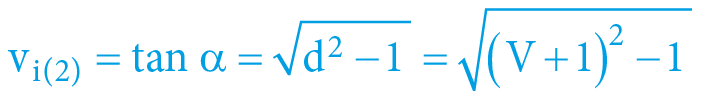
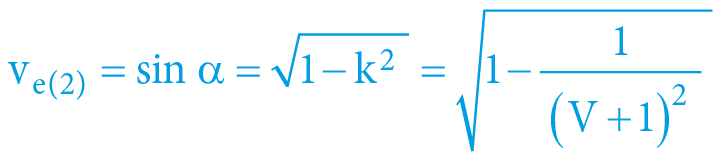
α = arcexsec V = arcsec d = arccos k = arcsin ve(2) = arctan vi(2)
Let’s note that thanks to the new system of units, the relation for the gravitational potential calculation was simplified (and rationalized). Gravitational potential and velocity are “dimensionless” – their unit is “1” – and thanks to this fact, they may be (as well as time contraction and dilation) used in trigonometry and its “unit” circle.
What “story” does the abovementioned trigonometry tell us about the spacetime angle (0.841 radians in this case)?
If there is a star with its gravitational potential equal to 0.5 (gravitational potential is determined by the exsecant function), then this gravitational field will “induce” motion of the surrounding objects and in the case of the free fall of this body (if insignificant mass) to this star, the impact velocity (to the star surface) will be equal to 1.118 from the internal point of view of the falling body (internal speed is determined by the tangent function), while from the point of view of an external observer (from the centre or from the surface of the star) the impact velocity of the body will be “only” 0.745 (external speed is determined by the sinus function).
The velocity difference is caused by time contraction of 2/3 respectively by time dilation of 1.5 (both values are “reciprocal” to each other as the cosine and secant functions), reflecting the fact that time flows slower to the moving object (faster from external view) – all of this is based on Euclidean geometry of spacetime.
The secant (describing time dilation) function also determines the externally seen increase in body mass 1.5-times and the exsecant (describing gravitational potential) function determines also the externally seen kinetic INCREMENT in mass by the value of 0.5-times of the rest mass (internal).
Logics as well as the trigonometric formulas tell us that the increase in mass (secant) is higher by one, than the kinetic increment (exsecant).
Therefore, the α angle is (within 4D spacetime) a primary “ratio of motion” – under the zero angle, the object moves only within its time component (the length component is zero).
Under the angle of the π/2 (90°) value, all the motion happens only within the length component – as within the internal optics of the moving object the speed is infinite (tangent) – whatever distance may be reached per zero time. For a human, this state of motion can’t be reached – in the universe, only photons “experience” it and we are only external observers, measuring the speed of 1 (sin π/2 = 1) – we call it “the speed of light is limited”.
From the mechanics point of view, all the existing matter in the universe is somewhere between these two states of motion and the abovementioned figure shows one of these states. Naturally, spacetime trigonometry is not only related to motions as a consequence of gravity – it works also for particles in accelerators, cannonballs or watches on your hands when driving the car – it works in general, whichever field (force) caused the motion.
In this (model) example, these standard universal “scenario” were somewhat “exaggerated” for the purpose of demonstration:
The close universe does not offer stars with such strong gravitational potential – our Sun would achieve it (0.5) only by compression of matter to a radius of ca 1×10-5 seconds (3 km).
We chose this example to confront it with a traditional physical scenario, which calculates the born of a “black hole” for these values.
Let’s note carefully – that within our expected “Euclidean” scenario – nothing “black” or “dark” is about to happen:
The impact (escape) velocity will be “below the speed of light” from our external point of view (0.745), while time dilation will be “reasonable” (1.5) and even the gravitational redshift (of the measured sun radiation on Earth) will not be “unlimited”, but ca 1.65 (z = eV).
So the Euclidean geometry of spacetime contradicts the existence of “black holes” – an unlimited shift of light (its disappearance) and apparition of some “singularities” would require unlimited gravitational potential, and that is ruled out within real space.
Some may feel disappointed…
If we come back to reality and return factual values to our Sun (radius of ca 2.3 seconds) the abovementioned trigonometry will be still functional, albeit it will be senseless to draw a triangle with an angle of 0.002 radians (we would see only two “parallel abscissas”). Therefore, a table will be sufficient and for imagination we will also add a column with “traditional” units:
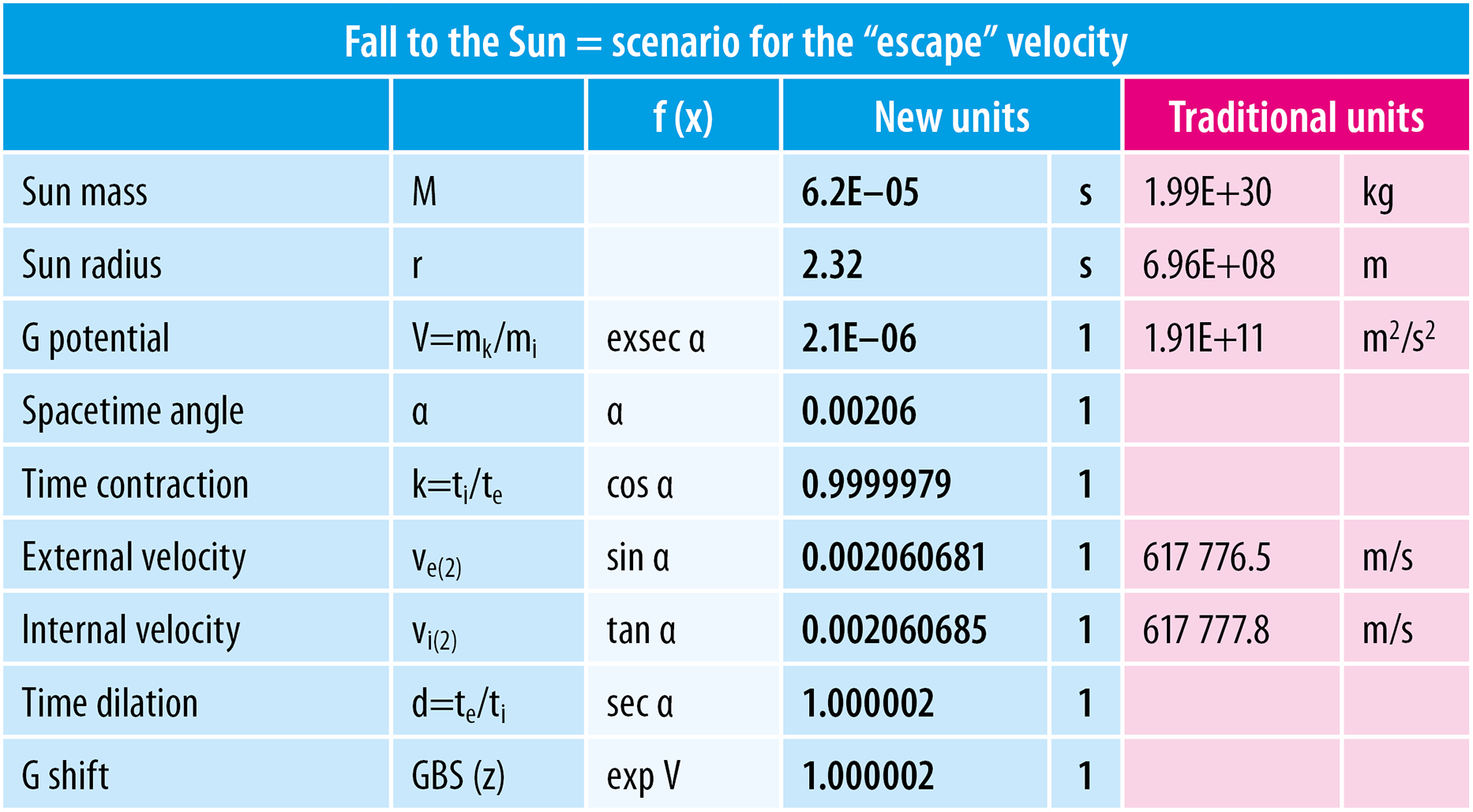
Table 16: Real values for our Sun
Each “lost” meteor will crash into the Sun with a speed of 0.002060681 (617 776.5 m/s), if the speed is measured externally from the Sun’s point of view (we will consider the initial meteor speed as zero). Due to the time contraction, the impact speed will reach 0.002060685 (617 777.8 m/s) from the meteor’s point of view. Within the “humble” forces of our Solar System – the time disproportions (4D spacetime) will cause a difference in the speed of only 4×10-9 (1.3 m/s), as the time will be deformed only insignificantly (d = 1.000002)!
Let’s note that the calculated speed of the meteor at the moment of its impact to the Sun (no matter whether ve(2) or vi(2)) is identical with the escape velocity specified for the Sun, as the “fall” to the Sun from such a large distance is a de facto “reverse” mechanism to shooting the body “beyond the borders” of gravity.
The following subchapter will reveal why the results of spacetime trigonometry within the close universe is de facto not different from traditional Newtonian physics:
5.1 SIMPLIFICATION FOR “SLOW” PHENOMENA:
So if the gravitational potential is relatively small (e.g. in our Solar System), the motion induced by gravity will be “slow” (not proportional to the speed of light). In such a situation – for small angles, the spacetime trigonometry may be neglected, as for very small numbers the following (approximately) shall apply:
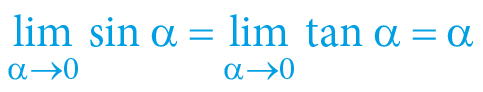
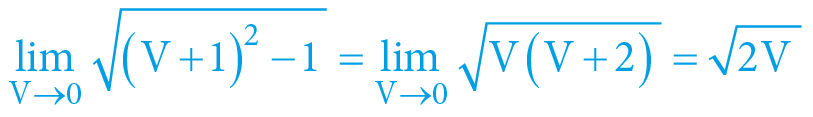
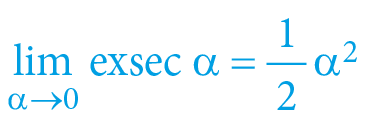
Therefore, in the case of “slow” phenomena, the spacetime trigonometry may be simplified – time is the same for everyone (time dilation and contraction are non-measurable) and analogically – speed is also the same for everyone. The relation of escape velocity on gravitational potential may be described by the (traditional) formula of Newtonian gravity (within rationalized units) approximately:
V = M / (4 π r)

The abovementioned limits (together) reveal to us why the “traditional” formula for kinetic energy works approximately:
For this example (real Sun), even the Newtonian formulas may apply, which will help us to calculate the impact velocity of that meteor in a very similar value of 0.002060684 (617 777.5 m/s) – the difference is only within 10-7 for internal speed and within 10-6 for external speed. Therefore – within our Solar System, we may rely on Newton with a relatively high accuracy (on the borders of actual metrology) – and the same applies to all of “our” planets.
However, in astrophysics, in general, we can’t rely on Newton – in the case of neutron stars, the 4D trigonometry provides completely different values (as it brings a different philosophy of mechanics and gravity), and we have already mentioned the existence/non-existence of Black Holes before.
If we want to summarize the abovementioned, then we can formulate the following:
THE FIRST LAW OF SPACETIME MECHANICS (1. LSM)
Everything exists in a Euclidean four-dimensional spacetime, consisting of three length dimensions and one time dimension.
6 SPACETIME TRIGONOMETRY AND MOTION SYMMETRY
Probably – our previous chapter upset many of those who know the Theory of Relativity:
“Motion exceeding the speed of light is against the first postulate! You ignore the length contraction completely! Moreover – may the motions be divided on the basis of an internal or external point of view? Such division is unacceptable! Motion is relative …”
So within this chapter, let’s focus on the “relativity principle” (and related limited speed thereto) and to reveal on what basis it can be OBJECTIVELY (not relatively) established which “observer” is in the position of an external passive observer and conversely, which one is an internal participant of the motion:
The response to relativists is tightly connected to the generalization of the scenario from the previous chapter together with another (used for centuries) “postulate”:
“An object either remains at rest or continues to move in a straight line at a constant velocity, unless acted upon by a force.”
Almost all people have been memorizing the abovementioned fundamental postulate of mechanics for centuries – either as the “Law of Inertia” or as “Newton’s First Law”. With all respect and appreciation to Newton … once and for all, it has to be modified significantly:
If we really want to understand the laws of motion, we have to get rid of an extreme focus on a single, separately moving object!
Even some predecessors of Newton came to the conclusion about constant (steady and straight-line) motion. But even in their case, this was only a formulation, which failed in ability to see the “relations” – because the “law” was made in the singular. We have to use the plural form!
The actual definition of the primary law of motion is a “half-definition” – it covers only half of real motion – only one side of the equation for each motion phenomenon, which is never one-sided:
The “law” described in actual textbooks describes the forward movement of a cannonball well, however it ignores cannon recoil. It describes forward movement of the space-ship, however it ignores the return flow of flue gas. It describes the forward motion of a kicked soccer ball, however it ignores the slowdown of the player’s body.
Naturally, Newton’s genius did not ignore these causality phenomena completely – it was defined as the Law of Action and Reaction (Third Newton’s Law), however this separate definition of two motion laws is inconsistent.
The unfortunate formulation of the main law of motion blinds us and our minds these days:
It speaks about one and only one body, while in the universe, there is no movement which would relate to only one single body! Although the additional “laws” reveal much to us, together they neglect a very important characteristic of motion, that:
Motion (of objects) is always symmetric in mass!
Any mass may move in space in a certain direction only “for the price” of other mass moving in an opposite direction. Although we can find this principle (now we call it the Law of Conservation of Momentum) even in Newton’s documents, it’s only a secondary consequence of his three motion laws – unfortunately.
The fact that mass never moves alone and that as a part of a “set” it always moves symmetrically, is not auxiliary – this is the primary law of motion! Only in this “light” – does it give physical sense to the motion of terrestrial and celestial bodies.
Thus, symmetrical motion of mass also gives sense to the question of whether motion is RELATIVE or ABSOLUTE:
THE SECOND LAW OF SPACETIME MECHANICS (2. LSM)
A set of locally isolated objects always move symmetrically in relation to its center of mass (barycentre) within 4D Euclidean spacetime, so the position of the barycentre remains preserved.
Objects do not exist alone – they are always a part of some local group of objects and this principle (belonging to a larger group) is repeated analogically by the inclusion of the entire universe. Velocity and space trajectory of any partial objects is always so symmetrical, that the position of the barycentre (of the local group of objects) remains preserved within the 4D (Euclidean) space.
Motion in relation to the local barycentre is always objective, absolute and primary motion of all the objects. Therefore, there is always one very important place in the space (frame of reference):
The barycentre is the one, preferred frame of reference – which is the (in terms of the previous chapters) external “observer” – it “stays at peace” and does not move – so the observed objects are limited in their speed from its point of view (see the sine).
From the opposite – internal perspective (objects observe their barycentre), their speed is not limited (see the tangent).
Motion is NOT relative!
And with this ABSOLUTE point of view of motion, we can return to the end of the previous chapter, where the “escape velocity” was discussed in the situation when the mass of a “central” body (star, planet) is completely mass dominant against the “insignificant” mass of “falling” objects.
In such case, we may “neglect” motion symmetry as well – the dominant body from the mass point of view may be considered as a non-moving body – it is de facto a barycentre – and only an “insignificantly massive” body takes part in the entire motion.
However, what will be the consequence within the spacetime trigonometry, if both bodies are with “significant” mass, and so it is necessary to count on the principle of motion symmetry?
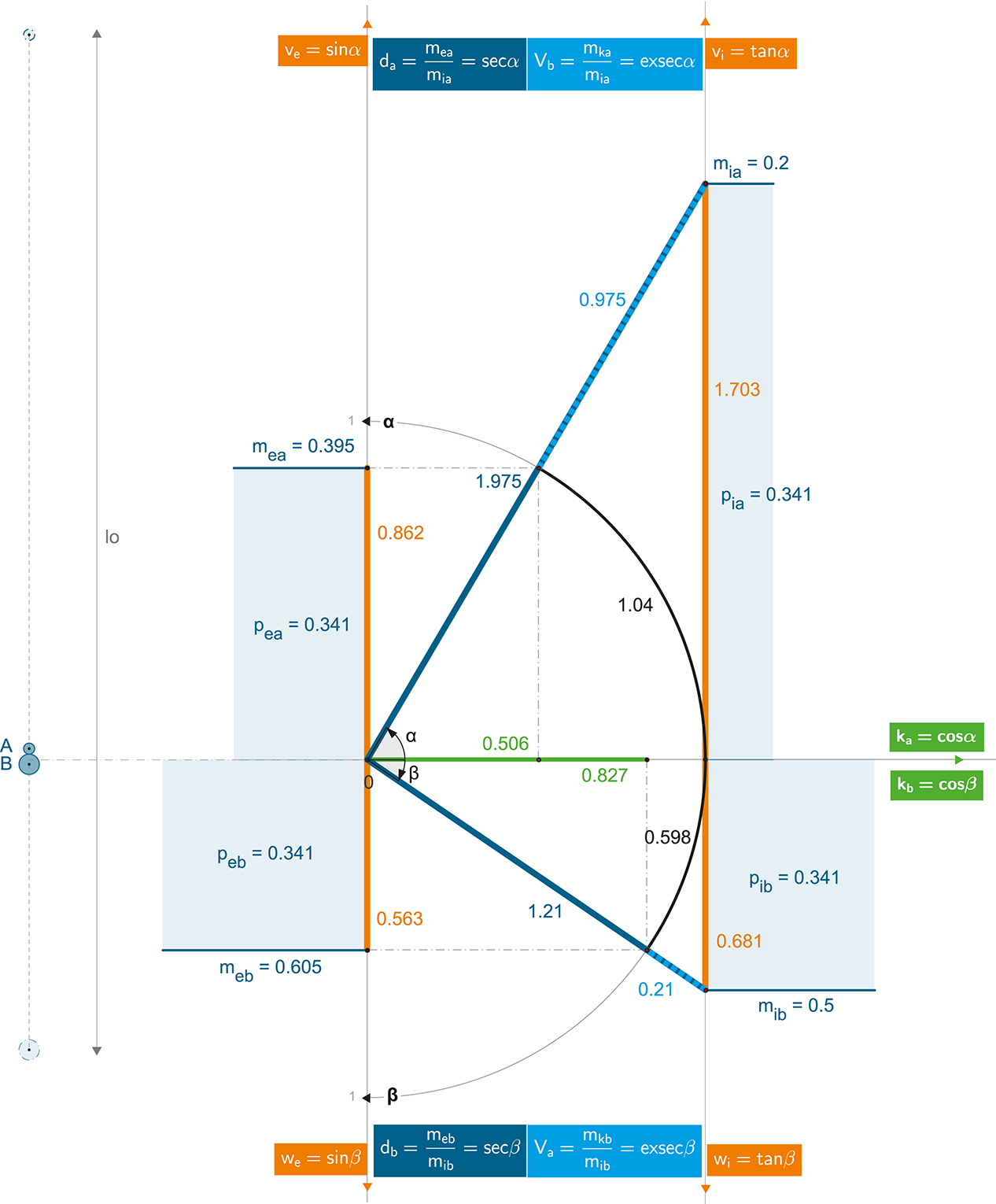
Picture 160:
INTERACTIVE ANIMATION
Two bodies (with comparable mass). The rectangular areas demonstrate the motion symmetry – momentum conservation.
αinduced spacetime angle of the motion of object A (in relation to the barycentre) [1]
βinduced spacetime angle of the motion of object B (in relation to the barycentre) [1]
Vagravitational potential of an “excited” object A (induced motion of the B object) [1]
Vbgravitational potential of an “excited” object B (induced motion of the A object) [1]
ve weexternal speed [1]
vi wiinternal speed [1]
k d time contraction and dilation [1]
mia mibinternal (primary, rest) mass of the object A and B [s]
mea mebexternal (apparent, total) mass of the object A and B [s]
mka mkbkinetic mass of the object A and B [s]
pia pibinternal momentum of the object A and B [s]
pea pebexternal momentum of the object A and B [s]
This chart displays the situation when two objects (A and B) of certain internal (rest) mass (mia and mib) and certain radiuses (ra and rb) within an original mutual distance (l0) will start to move to each other due to gravity (to their common barycentre); it quantifies the crash situation (at the moment when the surfaces of both objects meet).
Conversely to the previous chapter – the gravitational potential of any (of these both) bodies may not be “neglected” – bodies “attract” each other – so even the movement has to be mutual!
Even in this situation, the dynamics of the objects is determined directly by their gravitational potential (of both bodies) – according to the spacetime trigonometry. Total gravitational potential of bodies is therefore shared in a way, such that the motion symmetry (Law of Conservation of Momentum) is preserved, within the 4D Euclidean spacetime:
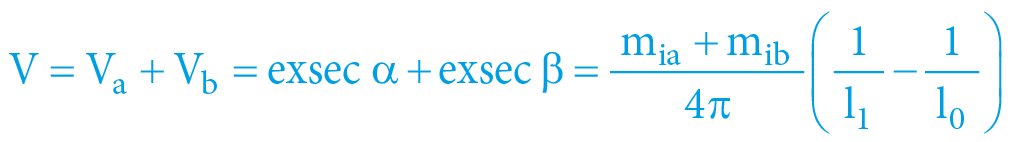
The mass symmetry of motion and Pythagorean trigonometry of spacetime allow only one solution for how to divide the entire gravitational potential between two bodies – see the abovementioned chart (the analytical solution of the Va and Vb calculation goes beyond the goal of this text).
It is again trivial to calculate all the searched values – both time dilation and (reciprocal) contraction, both internal speeds and both external speeds – we will calculate it easily on the basis of discovered spacetime angles – according to the spacetime trigonometry:
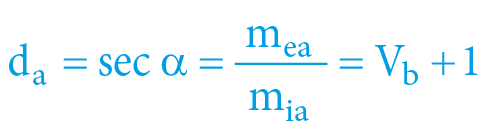
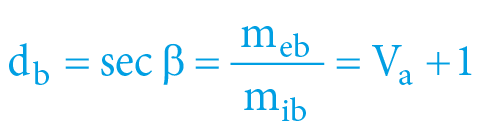
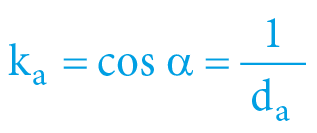
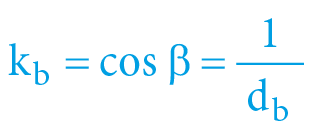
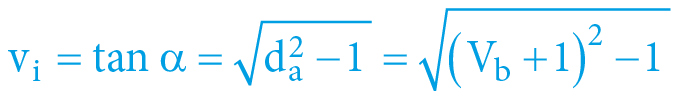
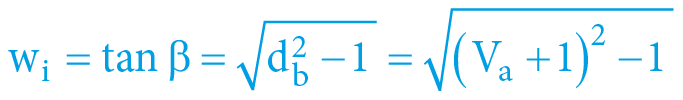
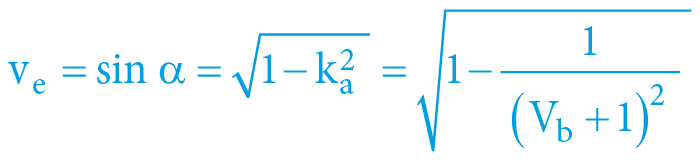
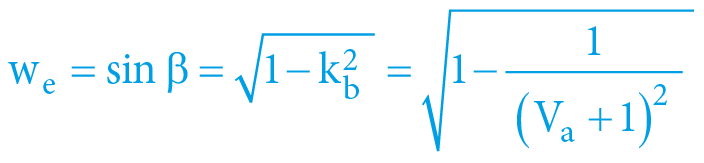
α = arcexsec Vb = arcsec da = arccos ka = arcsin ve = arctan vi
β = arcexsec Va = arcsec db = arccos kb = arcsin we = arctan wi
The previous equations reveal the speeds of both objects in relation to their barycentre and the values measured from the opposite perspective. But what speed will the objects measure to each other?
This derivation goes beyond the frame of this text, however even in this case, this task has an analytical solution:
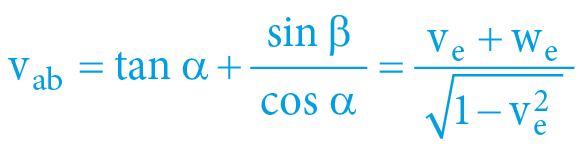
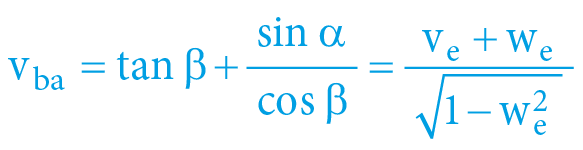
The situation is clearly described in the following table:
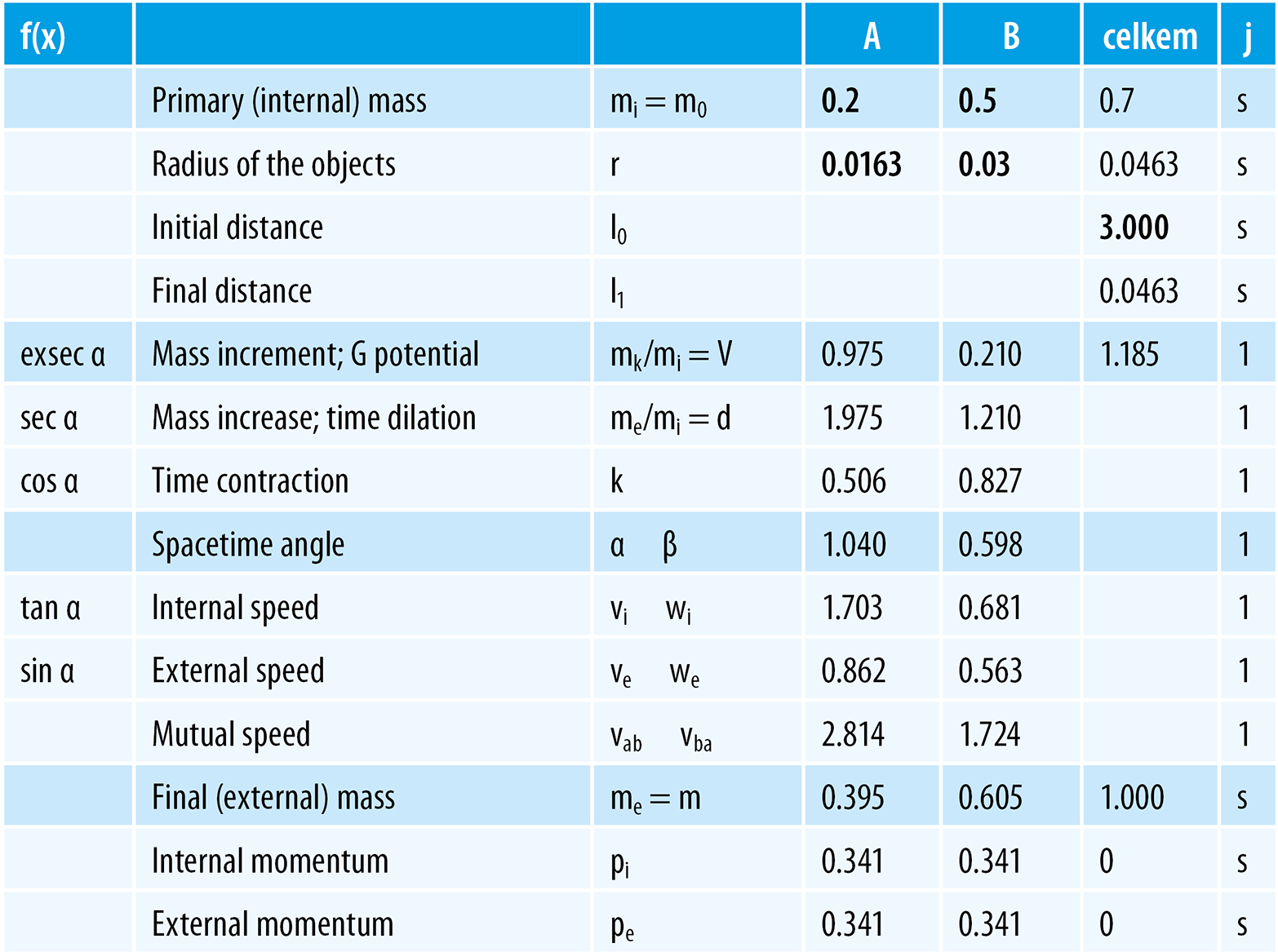
Table 17: Task and results
Both objects will move with “high speeds” (as both produce very strong and similar gravitational potential):
At the moment of impact – the speed of object A will be equal to 0.862 (2.6×108 m/s) from an external barycentre point of view, while from the opposite perspective (of an internal observer), object A will be moving to the barycentre by a speed of 1.703 (5.1×108 m/s) – this difference will be based in time disproportions (d = 1.975).
At the moment of impact – the speed of object B will reach 0.563 (1.7×108 m/s) from an external barycentre point of view, while from the opposite perspective (of an internal observer), object B will be moving to the barycentre by a speed of 0.681 (2×108 m/s) – this difference will be based in time disproportions (d = 1.21).
The mutual speed – where object A measures the speed of object B – will be 2.814 (8.4×108 m/s). From the opposite perspective (B measures the speed of A), the speed will be equal to 1.724 (5.2×108 m/s).
The principle of motion symmetry is shown here in the fact that from an internal or external point of view – the Law of Conservation of Momentum will work (in the chart, momentum is expressed by the area in rectangles) – everyone will agree (external and internal observation) on the measured momentum – the “set” of objects will be constantly “balanced”.
Of course – we have to emphasize that the universe today is so “diluted” that the abovementioned situation may not happen de facto – in a close universe, we will never find such massive objects (such a strong gravitational field). Macro-objects in the universe do not move by speeds close to the “speed of light” – therefore, in a real universe no relevant time disproportions occur during the movement of celestial macro-objects!
So it is necessary to formulate the following:
THE THIRD (SUM) LAW OF SPACETIME MECHANICS (3. LSM)
Matter of objects is not space bordered – the matter of each object penetrates through the entire universe in the form of a gravitational field.
Matter generates gravitational potential, whose decrease is inversely proportional to distance. This gravitational potential induces kinetic energy in the surrounding objects – induces their motion. This phenomenon is called gravity.
Due to gravity – locally isolated objects move through the 4D Euclidean spacetime symmetrically in relation to their barycentre (on curves) so the position of this centre remains preserved in space.
7 WHY NOT MAKE IT EASIER?
If we use the analogy with economics (the older sibling of physics) again – it provides an interesting lesson:
If we want to (at the beginning of the third millennium) perform global analyses in the economy (over nations or commodities) – we always use just one (mutual) unit, which is a factual prerequisite of meaningfulness and resulting clarity. To see the relations – we have to calculate everything in the same unit (the same currency).
Naturally, this principle should apply to physics as well!
Unfortunately – these days, physics is in the same situation as economic sciences were some centuries ago, when silver was exchanged for beads and black pepper was paid in gold. Now, physics is standing in front of the necessary procedure of “rationalization” of its units (and “rationalization” of number of constants) as well – the popular custom of naming a certain physical unit after each authority is unbearable anymore from the current perspective.
So – if we choose the second as the unit of time (since 1967 exactly defined by Louis Essen and cesium atom), then the same second should also be used for the other values of mechanics … if we want to see and understand more!
So – if we have been speaking about “mass and energy equivalence” for over 100 years, isn’t it now time to merge these two terms? Is it really necessary to persist on the constant of the value of 299 792 458 (c = 299 792 458 m/s)? Why overload physics (and memory) with the useless gravitational constant (G = 6.67408×108 m3 kg−1 s−2)?
Why not make physics easier?
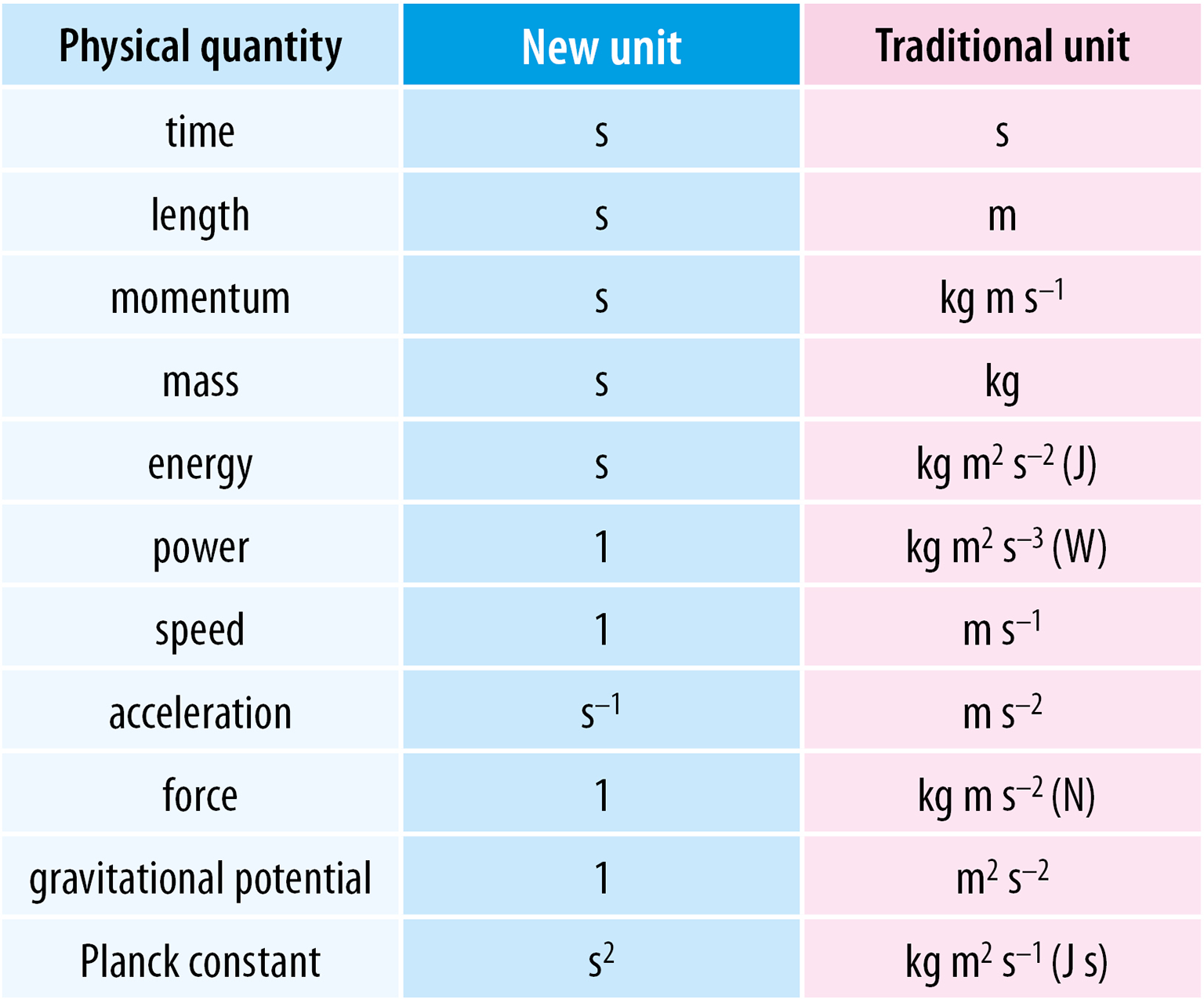
Table 18: In mechanics, it is possible to measure everything in seconds or in a dimensionless way! Old school fans may re-calculate everything in “traditional” units, of course.
The table above shows 11 essential physical “categories” of mechanics together with 11 traditional units. With only a little effort – these 11 categories may be measured just by 4 variations of only one physical unit – by the second or in a dimensionless way!
As a bonus – it is possible to eliminate (leave) 2 useless physical constants (speed of light in a vacuum, gravitational constant) and to simplify many physical formulas:
For example – for momentum, mass and energy of a photon, only one formula we can use in the future (h × f) and only one unit (second). Of course – by using these new units – the Planck constant will also get a “new” value and dimension (h ≐ 2.3×10-85 s2).
Mechanics may be almost as identically “perfect” as mathematics (the most general, abstract and objective queen of science). It is necessary to choose only the size of measurement scale (we have chosen the second) and mathematics will easily allow physicists to calculate (or draw) everything – to quantify and display it within the selected measurement scale – as easily as we can calculate (or draw) a right-angled triangle!
To understand spacetime, time disproportions and the phenomenon of gravity – we can reliably use proven and 1000 years old mathematical knowledges (Abul Wafa, Al-Birúní, Persia). We will use the “simple” trigonometry, which helped us to map our birth planet and identify her place within the universe:
Let’s imagine a neutron star, whose gravitational potential equals 0.3 (in new units).
Everyone agrees on the existence of neutron stars (unlike the case “black hole”). How difficult is it to determine the “escape” (impact) velocity on the surface of such a neutron star? How will the time (of a falling object) be slowed down?
We can take a calculator into our hands (one with trigonometric functions will be able to generate the results in one step) or we can place a blank sheet of paper, ruler and a drawing compasses on the table … and make a couple of simple steps:

Let’s draw a segment line, 1.3 (e.g. 13 cm) long …

… and next draw a circle through “1”.

Let’s make a tangent to the circle …
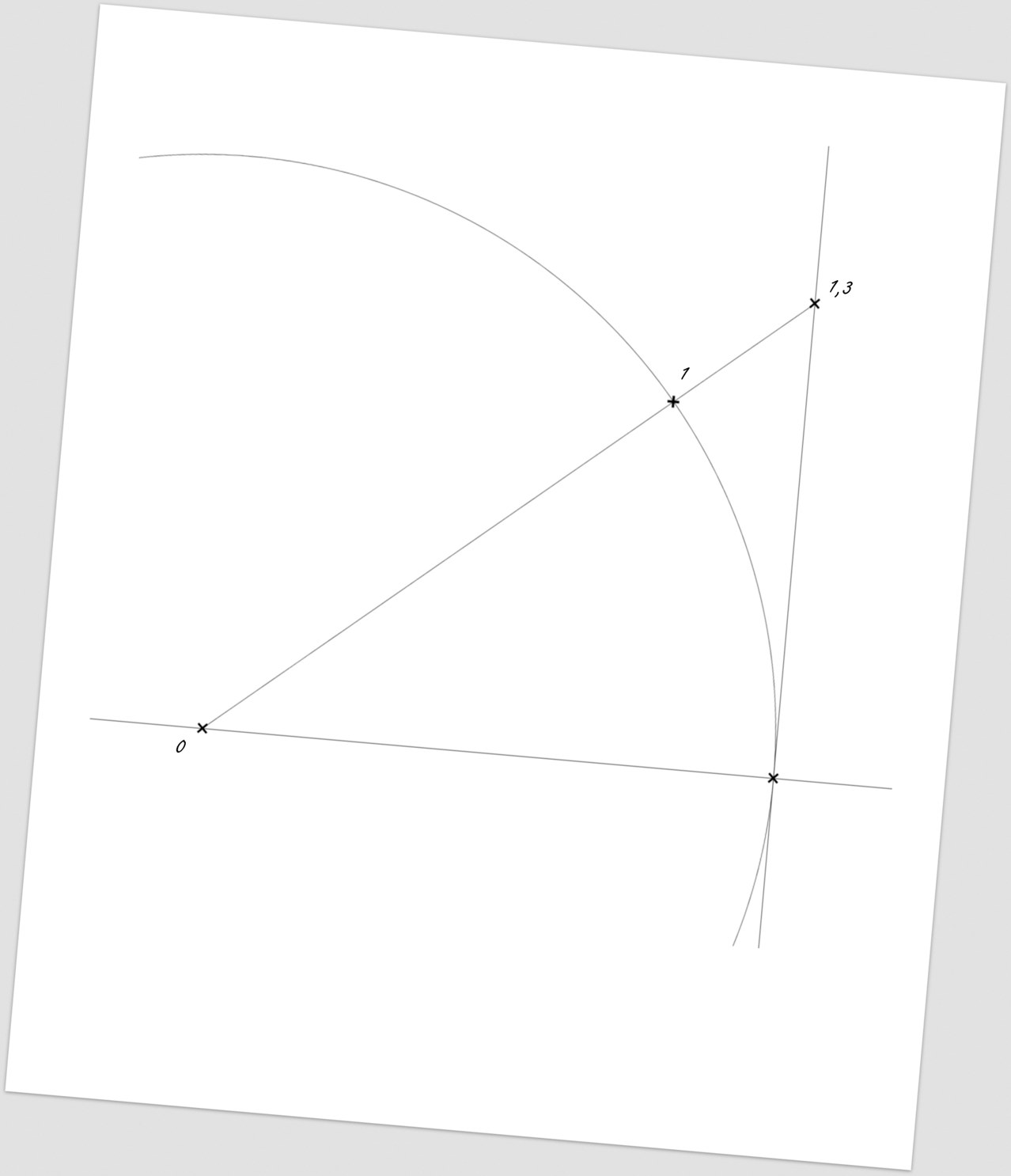
… and subsequently a perpendicular to this tangent (drawn through the circle centre) – thus, we will achieve the “x” axis.
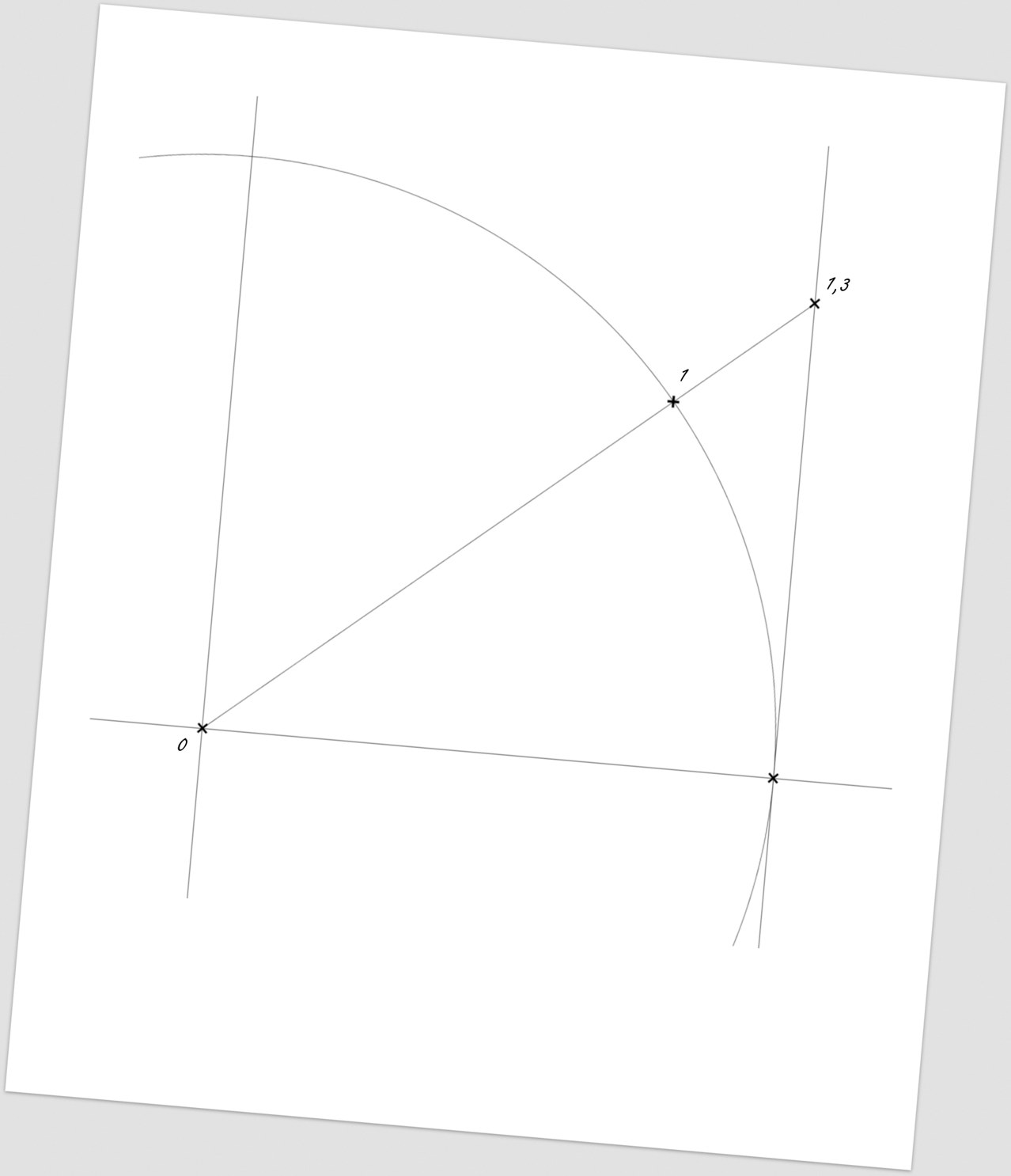
Another perpendicular line (through the circle centre) will complete the “y” axis.
Through the point “1”, we will draw lines parallel to each axis – thus, we will achieve the answer to all the questions regarding neutron stars.
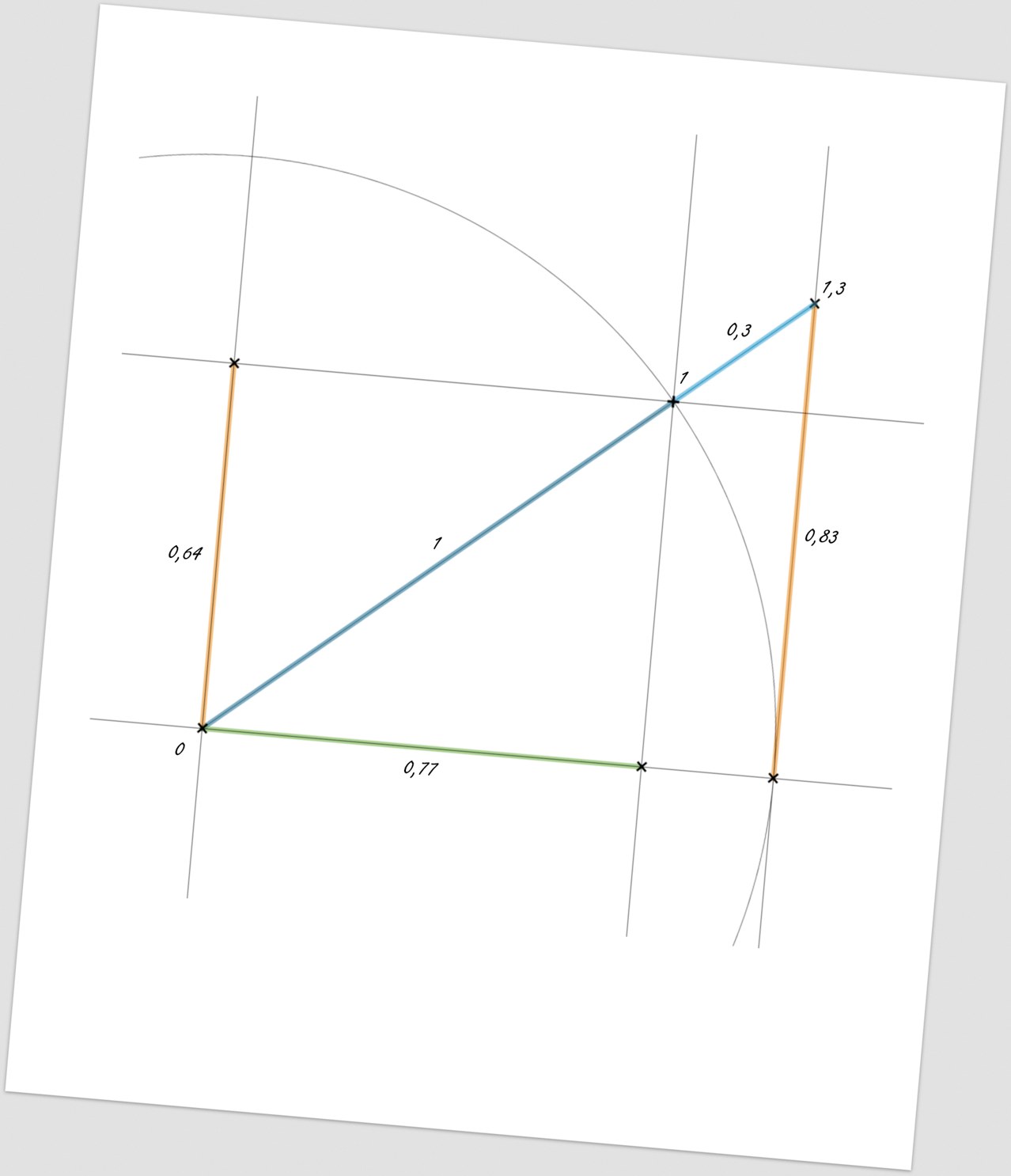
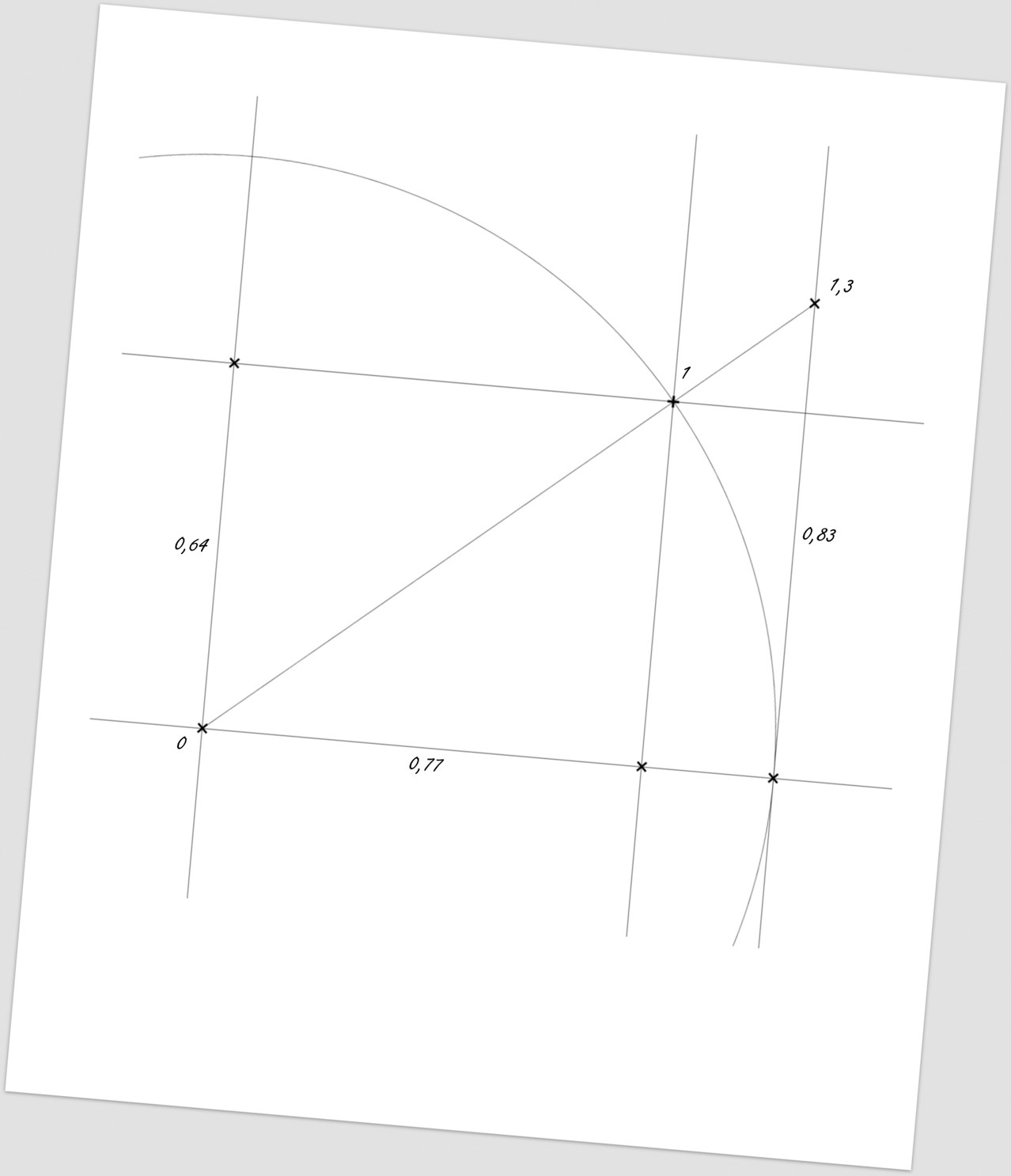
Picture 161:
Finally, we will measure the searched values, write them into the drawing and we can make it all clear by drawing it out in some colors.
In such (specific) case, it is possible to determine that the “escape” (impact) velocity will be 0.64 from an external observer’s point of view; 0.83 from an internal observer’s point of view and the time dilation/contraction will be 1.3/0.77 depending on who performs the time comparison (internal/external observer).
On a paper – we will solve the entire task with accuracy to one decimal point, while within a computer draw program with an accuracy of 3 decimal points and if we “draw” everything by using the Geogebra software, even to 15 decimal points!
Yes:
Mathematics of a “simple” right-angled triangle reliably describes space mechanics, mysterious spacetime and the phenomenon of gravity… nothing more is needed. It is almost embarrassing – physically and mathematically easy – banal and trivial – no rocket science!
8 MANY THINGS ARE COMPLETELY DIFFERENT …
The chapters before have already pointed to the fact that the Euclidean view of spacetime and related mechanics is just partially compatible with the current state of physics and the Theory of relativity:
Only certain trigonometric relations (their Pythagorean interpretation) are in line with the Theory of relativity – see time dilation, relativistic mass and relativistic momentum. Here, both theories result in the same mathematical formulas (tested by many experiments) albeit the theoretical fundament of both theories is different and new laws of spacetime mechanics (LSM) can’t agree with the relativists even on the relativity principle:
YES – the same physical laws for the entire universe – any “frame of reference” may be used for their description.
NO – motion is not relative!
With regard to the Law of symmetrical motion (2. LSM):
We can’t consider the formulations “train moves with the speed of 100 km/h” and “train station moves with the speed of 100 km/h” as “equivalent” – not even within “inertial frame of reference”. Local barycentre (Earth centre of gravity) assigns the position of an internal participant of movement to the train staff OBJECTIVELY, while people on the station platform watch everything just as external observers – with regard to the Earth mass, the station reciprocal (symmetrical) motion (with the Earth) will be de facto zero!
So – the measured time differences will also be objective – the internal participant will measure a shorter time (see cosine), therefore a higher speed (see tangent); the external observer will measure a longer time (see secant) therefore a proportionally lower speed (see sine).
In general – speed from the internal participant point of view will always be unlimited in principle (see tangent), while from the position of an external observer – speed will be limited (see sine).
Naturally, this is all related to the fact that the lengths (3D space distances), according to LSM, are invariant within the entire universe – the distance from the Earth to the Moon (1.3 seconds) is the same for everyone!
In comparison with the General Theory of Relativity (GTR), new laws of mechanics are even less compatible:
While the GTR explains the gravity phenomenon by a curved (non-Euclidean) spacetime, LSM defines gravity by using a basal (Euclidean) trigonometry – by using just one mathematical operation (exsecant)!
Both theories are numerically compatible with Newtonian physics for weak gravitational fields, however for a stronger gravitational potential, both theories are totally different – the GTR finally ends in an infinite/zero physical values and alibistic singularity (Black hole, event horizon, … ).
Within “usual” levels of gravity (according to our Solar System), both theories are almost equivalent from the quantitative point of view (differences measurement are limited by actual metrological technology) – gravitational frequency shift of the EM radiation (Pound Repka experiment, GPS compensation, …) or any other (meaningful) experiments may not reveal the reality by now.
However – even these days, we can use the trigonometric function exsecant (secant decreased by one) to express (in a general way) the kinetic mass increment, which (in the case of gravitational movements) is directly defined by the gravitational potential.
It’s also necessary to remind once again (in the goal of reaching a simplified and better physics), that it is necessary to modify the First Newtonian Law of Motion, and further still – to formulate it in plural form!
None of the bodies (in the universe) moves as a single body (without causality relation to some motion of other bodies) and not even by a “straight-line” motion – by its inertia (without the force effects)! And as there are more than two material objects in the universe – celestial bodies do not move even within conic sections:
New Law of Inertia (re-formulation of the 3. LSM):
Free of any external forces (by inertia) – bodies move through the Euclidean spacetime symmetrically over the curves, whose trajectory is defined by the local gravitational potential of all the surrounding bodies in such a way that preserves the position of their barycentre.
9 … AND MANY THINGS REMAIN UNKNOWN
Despite all the previous chapters… we have to humbly repeat the “I know that I know nothing…” from Socrates and highlight the fact that many important and fascinating questions remain:
The age (duration) of the universe is estimated to be ca 0.4×1018 seconds (14 billion years). The length radius of the universe, known (visible) to us is estimated to be ca 1.5×1018 seconds (46 billion of light years). The matter of the observed universe (without the “dark forces”) is estimated at ca 4.7×1018 seconds (1.5×1053 kg)!
Isn’t this 1018 order match “suspicious”?
Only within this context, we can finally realize that the unit newly defined for mass (second) is “large” only ostensibly – it is “timely” and “longitudinally” proportional. The size (gigantic or insignificant) is relative from this point of view (in its correct sense):
The value of mass second (3×1034 kg) is the same large/insignificant mass as the time second is large/insignificant within the entire history of the universe’s – as well as the length second is a large/insignificant distance in comparison with the size of a visible universe.
The order of magnitude for all tree “seconds” is de facto identical (1018) within the entire universe – if we speak about the time (duration), length (size) or mass (matter, energy)!
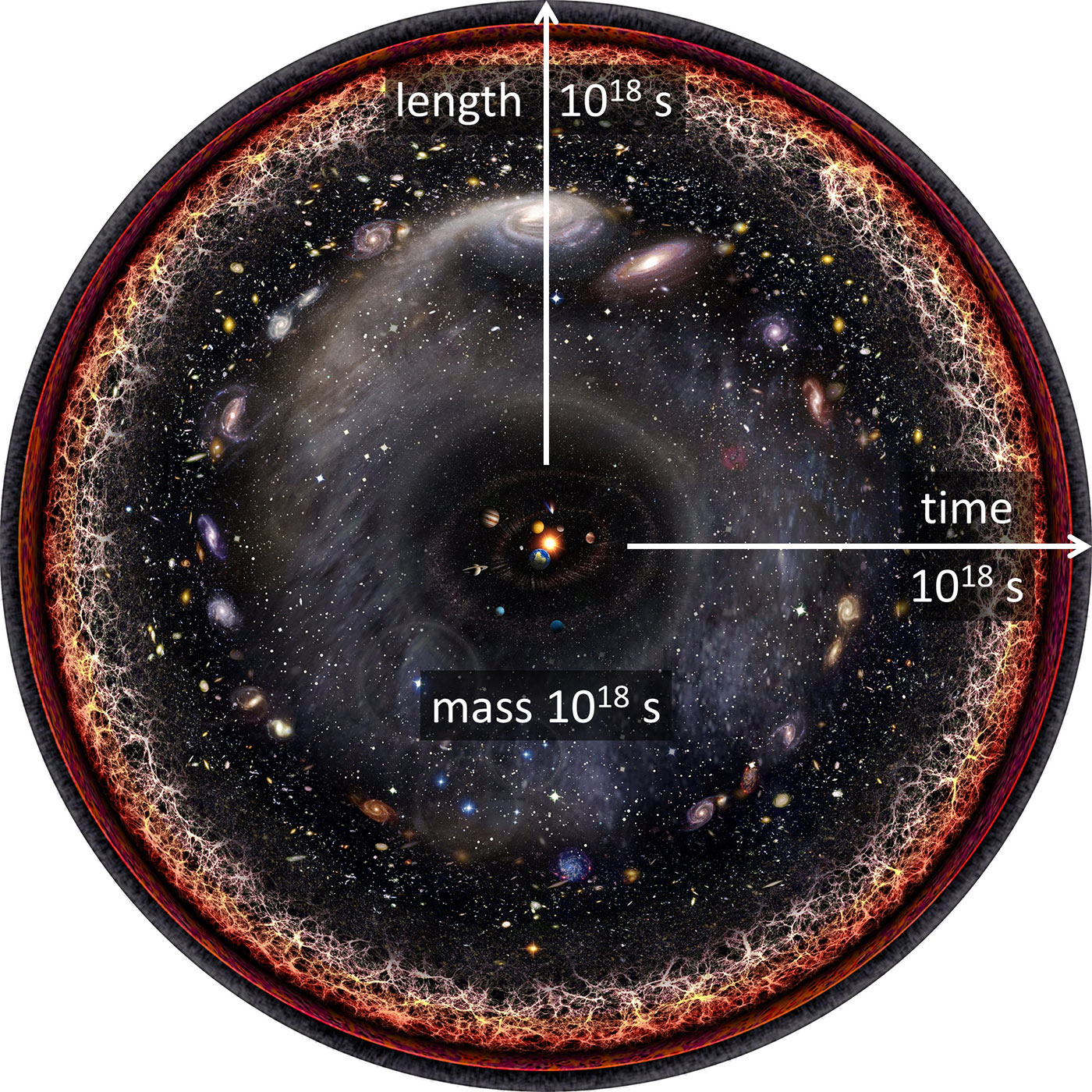
Picture 162:
Second defines the “broadness” of (the only one) our “basal physical unit”!
(Source: Wikimedia)
Note:
The abovementioned values for mass, distance and duration of the universe have to be considered with “sufficient margin” – they are the result of an actual cosmological model, where there is more “unknown” than what we “know”.
Therefore, the mentioned numbers should not be considered as dogma – with certain care, they may have some “order of magnitude” validity.
Despite the unknown to us (more valid numbers related to the duration, size and mass of the universe)… this order of magnitude concurrence (in case we measure everything in seconds) is surprising, but also fascinating:
• Is it only a coincidence?
• What does the universe want to tell us thereby??
• What if the universe is as “massive” as it is old, as it is big???
Was the second always the same? How about in the times when the universe was as old (and large) as only 107seconds? Was the second equal to the 9 192 631 770 period of the radiation corresponding to the transition between the two hyperfine levels of the ground state of the cesium 133 atom, at that time as well?
And was the universe at that time massive within the order of 1018, or 107?
And other very important questions occur again:
Which “particles” intermediate the gravitational interaction? The Theory of relativity is incompatible with quantum physics (gravitation is caused by spacetime curve, and therefore – it is nonsense to search for such a particles of gravitational interaction), however the Euclidean interpretation of spacetime opens the door to quantum physics again.
When will they reveal the gravitational interaction particle in Cern?
It is obvious that even tomorrow – many more questions than answers will occur!
“It’s what we think we know that keeps us from learning!”
Claude Bernard
However, even today – the “universal” use of the second can help us to perceive the “size” of the visible universe better:
From the human mind point of view, we have a relatively clear idea of how long one second lasts – our intellect can compare it with the long (but still imaginable) duration of the universe (14 billion years) pretty well.
The awareness, that in the same ratio, we can also perceive the size of the universe, where one second corresponds roughly to the distance to the Moon…, and the mass of the universe may be perceived in the same way, where our Earth has a mass of only 0.2 nanoseconds … may help everyone to better “visualize” the surrounding universe and our position therein!
10 FINAL DENOUEMENT
The question remains, if this text is sufficiently “crazy” so even the actual mainstream physics takes note of it:
Following the LSM – spacetime is not curved in any way (it’s only a boring, Euclidean spacetime), contractions of length are condemned and “black holes” seem to be completely unreal.
Motion can’t be perceived “relatively” anymore. Thus – physics will be missing a few “traditional” paradoxes and the mathematical system of 4D spacetime mechanics would become reduced to only a basic trigonometry.
Also, mechanics would lose two “basic” physical constants, the number of physical units would decrease and thus, many related formulas would be simplified.
The gravity phenomenon may be easily clarified by a ruler and drawing compasses!
…many experts would protest …
But it’s only a matter of time before physics will implement the idea that the world should not be made more complicated, … and thus – once we accept the fact that (inter alia) the Moon is at a distance of 1.3 seconds and has a mass of 2.3 picoseconds.
We should always be making our world more and more simplified!
The hypertrophic number of physical units and constants has already been creating chaos in the heads of students for centuries. Even in 2017 – textbooks write about 7 “elementary” physical units, tens of “derived” units and a number of “constants”. But the truth about the base of physics is trivial and completely clear:
If any modern land surveyor wants to measure the LENGTH of land (never mind whether in meters or yards), he uses satellite navigation, therefore the principle is based in TIME measurement … and if it’s necessary to establish the MASS of an astronaut on a hi-tech ISS space station (doesn’t matter whether in kilograms or pounds), they will attach him to a “spring chair” and measure the frequency of free vibrations, so the TIME!
Therefore – only one elementary physical unit exists!
Let’s stop entropy increasing in the heads of our students … Physics may be much easier and so even more beautiful … there is only one[1] elementary physical unit – only one elementary physical quantity:
TIME!
TK; December, 2017 The author is an economist and in 2016 he published his first (Czech) edition of Time theory. ________________________________________________________________________[1]Yes – “second” is the elementary (primary) unit not only for mechanics. With the same advantage, second may be used for the measurement of other physical values (clarification goes beyond the goal of this text) as well.

